CALCULO DEL COEFICIENTE DE PERDIDA DE FRICCIÓN
DEFINICIÓN
DEL FACTOR DEL FRICCIÓN.
El factor de fricción f sin dimensiones y que tiene
relación con respecto al material de la tubería (Por ejemplo PVC. fe, acero inoxidable,
concreto, etc) y estará en función de (r, D, E, m,n ).
CALCULO DEL FACTOR
DE FRICCIÓN EN RÉGIMEN TURBULENTO Y TUBERÍA RUGOSAS.
En las tuberías rugosas, si el número de Reynold
es bajo (Re<2000, o Re>2000 pero de manera que el flujo sea laminar), la
rugosidad no influye en la pérdida de carga y :
f = F(Re)
Si el número de Reynold es elevado, por el contrario f deja de
ser función de Re y se tiene:
f = F (K/D)
Si el número de Reynold tiene un valor intermedio se tendrá en general
f = F (Re, K/D)
Donde K es el valor de rugosidad efectiva.
La mayor parte de los conductos de agua que han
estado en el servicio durante varios años sufren alguna reducción en su capacidad de
conducción, debido a las incrustaciones o al revestimiento de limo que tiende a
depositarse sobre la superficie interna. El índice de deterioro depende de la
constitución química del agua y del material de la tubería. Por tanto cuando se
proyecta un conducto de agua, es prudente tener en cuenta las condiciones probables en
que se encontrará después de un período de años de servicio
Colebrook y White, mediante una simple aplicación de su Ley de
Transición, demostraron que si la rugosidad aumentaba desde K = 0,01 pulg. en una
tubería de 20 pulg. la capacidad de conducción se reducía en un 25%. Sin embargo la
reducción correspondiente del área de la sección sería de sólo un 2% aproximadamente.
Parece razonable deducir que la reducción de la capacidad de conducir se deba
enteramente al aumento de la rugosidad con la edad de la tubería; los exámenes y ensayos
de la tubería confirman la solidez de esta hipótesis.
Analizando los datos de los ensayos sobre tuberías de fundición, Colebrook y White
dedujeron que la rugosidad aumenta uniformemente con la edad y por tanto puede expresarse
correctamente mediante la sencilla fórmula empírica;
K = Ko + a t
Donde, Ko es la rugosidad efectiva inicial, K
es la rugosidad efectiva después de t años y a es el
índice de aumento anual de la rugosidad.
Lamont y otros investigadores han demostrado que estas formas de ecuaciones son
aplicables a otras clases de tuberías, el valor de a puede obtenerse
de tablas o de ensayos realizados a intervalos periódicos de tiempo.
Nikuradse, experimentó con tuberías de
rugosidad artificial obtenidos con granitos de arena esféricos de diámetro K controlados
exactamente con los que recubría interiormente la tubería. Como una protuberancia
pequeña puede ser insignificante en una tubería grande, la variable representativa del
fenómeno no será K, la rugosidad absoluta, sino K/D ó rugosidad
relativa. Los valores más corrientes de K/D oscilan entre 0,0333 y 0.000985 en las
tuberías comerciales.
La rugosidad natural de las tuberías comerciales (Hierro fundido, hormigón, etc.) es
naturalmente irregular, sin embargo la rugosidad absoluta de una tubería comercial se
puede caracterizar también por un valor K que es igual al diámetro K de los
granitos de arena de una tubería de rugosidad artificial que diera el mismo valor de
f para un número de Reynold suficientemente elevado.
Los trabajos de Nikuradse sirvieron para deducir las siguientes ecuaciones:
Calculo del Factor
de Fricción en Régimen Turbulento y en Tuberías Lisas (2 000 < Re< 10
000): Fórmula de Blasius.
Como las tuberías son lisas, f no es función de la
rugosidad relativa, K/D, ya que ésta es nula (K=0) o sea que f = F(Re), en este
caso se aplica la ecuación de Blasius:
f = 0,316/Re
Cálculo del
Factor de Fricción en Régimen Turbulento y Tuberías Lisas para Re >100
000: Fórmula de Karman - Prandtl
Para régimen turbulento y
tuberías lisas también, pero para Re> 100 000; con estudios teóricos y
ajustando los coeficientes experimentalmente, Karman - Prandtl
dedujeron la primera Ecuación de Karman - Prandtl:
Cálculo del
Factor de Fricción para Tuberías Comerciales o de Rugosidad Natural
Segunda fórmula de Karman - Prandtl y la
ecuación de Colebrook White. En una zona de transición en que f = F(Re, K/D),
se cumple la ecuación de Colebrook White:
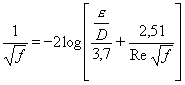
Esta es la fórmula universal de pérdida de carga en los conductos industriales. Los problemas prácticos con frecuencia se encuentran en esta zona de transición. A número de Reynold tanto más elevado cuanto la tubería es más rugosa se cumple la segunda ecuación Karman - Prandtl:
1/f = 2 log ( r/K + 1,74)