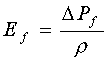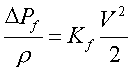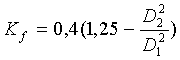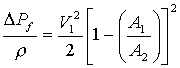DISPOSITIVOS PARA
MEDIR CAUDAL Y VELOCIDAD DE FLUIDOS
1.
TUBO VENTURIMETRO
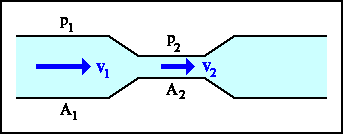
Es un tipo de boquilla
especial, seguido de un cono que se ensancha gradualmente, accesorio que evita en gran
parte la pérdida de energía cinética debido al rozamiento. Es por principio un medidor
de área constante y de caída de presión variable. En la figura se representa
esquemáticamente un medidor tipo Venturí.
2. MEDIDOR DE ORIFICIO
El medidor de Orificio es un elemento más
simple, consiste en un agujero cortado en el centro de una placa intercalada en la
tubería. El paso del fluido a través del orificio, cuya área es constante y menor que
la sección transversal del conducto cerrado, se realiza con un aumento apreciable de la
velocidad (energía cinética) a expensa de una disminución de la presión estática
(caída de presión). Por esta razón se le clasifica como un medidor de área constante y
caída de presión variable.
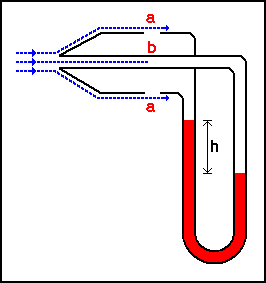
3.
TUBO DE PITOT
Es uno de los medidores más exactos para
medir la velocidad de un fluido dentro de una tubería. El equipo consta de un tubo cuya
abertura está dirigida agua arriba , de modo que el fluido penetre dentro de ésta y suba
hasta que la presión aumente lo suficiente dentro del mismo y equilibre el impacto
producido por la velocidad. El Tubo de Pitot mide las presiones dinámicas y con ésta se
puede encontrar la velocidad del fluido, hay que anotar que con este equipo se puede
verificar la variación de la velocidad del fluido con respecto al radio de la tubería
(perfil de velocidad del fluido dentro de la tubería).
4. ROTAMETROS
Es un medidor de caudal en
tuberías de área variable, de caída de presión constante. El Rotámetro consiste de un
flotador (indicador) que se mueve libremente dentro de un tubo vertical ligeramente
cónico, con el extremo angosto hacia abajo. El fluido entra por la parte inferior del
tubo y hace que el flotador suba hasta que el área anular entre él y la pared del tubo
sea tal, que la caída de presión de este estrechamiento sea lo suficientemente para
equilibrar el peso del flotador. El tubo es de vidrio y lleva grabado una escala lineal,
sobre la cual la posición del flotador indica el gasto o caudal.
Los rotametros, flowmeters, del tipo
area variable, son instrumentos diseñados para la medición y control de caudales, gases
y líquidos. Fabricamos caudalímetros desde 1 ml/h hasta 1000000 lts/min. La unidad de
lectura vendrá especificada en la unidad de preferencia del usuario (lts/h, g/min,
mtr^3/h, scfh, lbm/min, scfm, etc, etc), es decir, lectura directa de caudal.
Rangos operacionales diponibles: desde 0,5 ltrs/h de agua (0,01 mtr^3/h de aire), para
tuberías de diametro 1/4" NPT, hasta 100000 ltrs/h de agua (3000 mtrs^3/h de aire)
para tuberías de diametro 4". Para diametros de tubería mayores de 3",
caudales hasta 10000000 ltrs/min, se usará el medidor de flujo de tipo area variable
modelo "push botton".
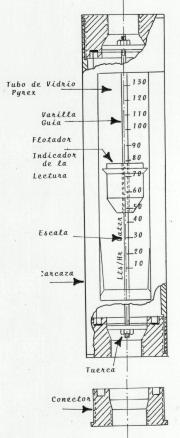
Aquí se presenta un
modelo de las especificaciones técnicas de un Rotámetro:
El tubo medidor del tipo pyrex, está protegido por una carcasa protectora de acero
inoxidable calidad 316.
EL flotador medidor se desplaza verticalmente a lo largo de una varilla guía, razón por
la cual pueden ser utilizados para medir fluidos de una alta viscosidad.
Rotametros de seguridad con fabricación especial y a requerimientos específicos están
disponibles.
Los materiales usados son:
Tubo medidor en vidrio borosilicato tipo pyrex.
Conectores y partes internas en acero inoxidable 316.
O-rines y empaques en teflón
La longitud de la escala medidora se ofrece en variados tamaños: 230 mm, 330 mm, 100 mm,
etc.
La precisión es del 2% en full escala.
5. MEDIDORES DE
DESPLAZAMIENTO POSITIVO
Son el fundamento o la base de muchos
elementos de control. El medidor de desplazamiento positivo es un instrumento sensible al
flujo. Este responde a variaciones en el valor del flujo y responde a señales mecánicas
correspondiente a la rotación del eje. Se aplican en las siguientes circunstancias: donde
se encuentre un flujo grande, donde se requiere una respuesta directa al valor de la
variación del flujo y donde la acción mecánica es necesaria.
BALANCE DE
ENERGIA MECANICA
La energía necesaria para bombear un
líquido a través de una tubería depende de una multitud de factores.
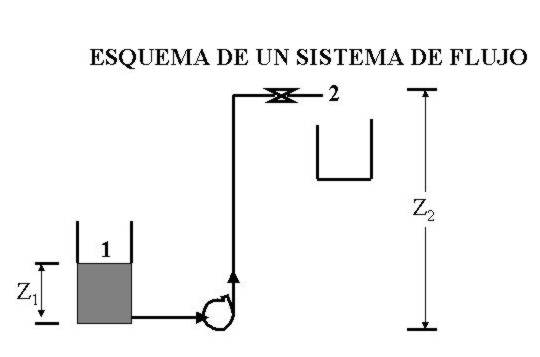
El esquema muestra que la energía necesaria para el bombeo depende de:
-
La fricción en la sección recta de la tubería.
-
La energía necesaria para mover un líquido de un punto a otro de
mayor altura.
-
La energía necesaria para mantener la velocidad de flujo deseada.
-
La energía necesaria para vencer cualquier diferencia de presión
entre la entrada y salida de la bomba.
-
La fricción creada por cambios en el área de la sección
transversal del flujo, uniones de la tubería, cambios de dirección y cualquier
rozamiento existente en el equipo necesarios para el sistema de transporte.
Estos
factores se analizan individualmente en este tema.
ENERGIA POTENCIAL
La energía
potencial es la energía necesaria para vencer un cambio de altura durante el transporte
de líquido. La expresión general es:
DPE = g ( Z2
– Z1 )
Donde
Z2 y Z1 son las alturas
indicadas en la Figura, la aceleración de la gravedad ( g ) sirve para convertir la
diferencia de altura en unidades de energía (J/Kg). Resulta evidente si el punto situado
aguas arriba está localizado por encima del punto de descarga, la energía potencial
ayudará a la bomba, reduciéndose la energía necesaria para el bombeo.
ENERGIA CINÉTICA
Para modificar la velocidad de un líquido que fluye la bomba debe
incrementar su energía cinética. Este
cambio puede expresarse como:
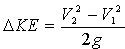
Donde al cambio está relacionado con la diferencia entre
las velocidades del líquido en los puntos a lo largo del sistema. En la mayoría de las
ocasiones la velocidad en el punto 1 será cero y las necesidades de energía serán las
requeridas para alcanzar la velocidad del líquido deseada.
ENERGIA DE
PRESION.
En algunos
sistemas de transporte la presión puede cambiar de
una posición a otra del sistema. Tales cambios puede incluirse en las necesidades de
energía como:
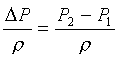
Donde se introduce a la
densidad del líquido para dar consistencia a las unidades de energía (J/Kg). Obsérvese
que la densidad del líquido no depende del tipo del sistema en que se analice.
ENERGIA DE FRICCION O
ROZAMIENTO
La pérdida de presión debida al
rozamiento a lo largo de una tubería recta se presenta
en la Ecuación de Fanny. La energía de
rozamiento o energía necesaria para vencer el rozamiento sería:
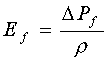
Cuando se trata de una tubería recta.
Otros componentes del sistema de
tubería también contribuirán a la pérdida de energía debida al rozamiento. Por
ejemplo un estrechamiento brusco en la sección de la tubería puede evaluarse como:
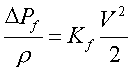
Siendo:
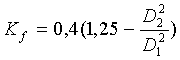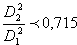
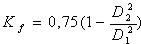Si
Si
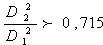
De manera similar, un aumento brusco en
la sección de la tubería contribuirá a la pérdida de energía debida al rozamiento.
Estas pérdidas pueden estimarse como:
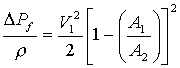
Donde
los parámetros que tienen los subíndices 1 se localizan aguas arriba de la expansión.
Todos los accesorios como codos, “tes”, y válvulas contribuirán a las
pérdidas debida al rozamiento. La contribución al
rozamiento de cada una de estas piezas pueden expresarse
como una longitud equivalente de tubería recta, Le y sumarse a la longitud real de la tubería. La
longitud equivalente de un accesorio puede calcularse seleccionando el valor
correspondiente de Le/D y conociendo el diámetro
de la tubería.
INTRODUCCIÓN
A LA REOLOGÍA
1.1
Reología
1.1.1 Definición
La Reología
es la ciencia del flujo que estudia la deformación de un cuerpo sometido a
esfuerzos externos .Su estudio es esencial en muchas industrias, incluyendo
las de plásticos, pinturas, alimentación, tintas de impresión, detergentes
o aceites lubricantes, por ejemplo.
1.1.2
Historia de la Reología
En 1678 Robert Hooke fue el
primero que habló de la reología en su libro “Verdadera teoría de la
Elasticidad” [1]. Dicha teoría se resumía en lo siguiente:“Si se dobla la
tensión, se dobla deformación”.
Nueve años después, Isaac Newton publicó en
“Philosophiae Naturalis Principia Mathematica” una hipótesis asociada al
estado simple de cizalladura (o corte): “La resistencia derivada de la falta
de deslizamiento de las partes de un líquido es proporcional a la velocidad
con que se separan unas de otras dentro de él”. Esta necesidad de
deslizamiento es lo que ahora se denomina “Viscosidad”, sinónimo de fricción
interna. Dicha viscosidad es una medida de la resistencia a fluir.
La fuerza por unidad de área que se
requiere para el movimiento de un fluido se define como F/A y se denota como
“s”
( tensión o esfuerzo de cizalla). Según Newton la tensión de cizalla o
esfuerzo cortante es proporcional al gradiente de velocidad (du/dy), o
también denominado como D. Si se duplica la fuerza, se duplica el gradiente
de velocidad:
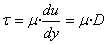
Esta fórmula se denomina Ley de Newton [2], que
es aplicable actualmente aún para unos fluidos determinados (Newtonianos).
La glicerina y el agua son ejemplos muy comunes que obedecen la Ley de
Newton. Para la glicerina, por ejemplo, la viscosidad vale 1000 mPa·s, en
cambio para el agua la viscosidad vale 1 mPa·s, es decir, es mil veces menos
viscosa que la glicerina.
En esta época apareció la Ley de Hooke que
fue de aplicación para el estudio de la reología de sustancias
sólidas:
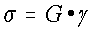
Siendo:
s
: esfuerzo cortante (Pa)
G : módulo de rigidez (Pa).
g
: deformación (%).
La fórmula nos dice que si se aplica una carga
s
sobre un cuerpo sólido, éste va a sufrir una cierta deformación
g.
El valor de dicha deformación se mantendrá hasta que cese el esfuerzo
aplicado.
Hace 300 años los estudios relacionados con la
Reología se reducían a aplicar la Ley de Newton para líquidos y la Ley de
Hooke para sólidos. Fue a partir del siglo XIX cuando los científicos
comenzaron a tener dudas acerca de la validez universal de estas leyes
lineales.
En 1835 W. Weber llevó a cabo una serie de
experimentos con gusanos de seda y vio que no eran perfectamente elásticos.
Lo que observó fue que una carga longitudinal producía una extensión
inmediata, seguida de un posterior alargamiento conforme transcurría el
tiempo. Al eliminar la carga se producía una contracción inmediata, seguida
de una contracción gradual de la longitud hasta llegar a la inicial . Estas
características se asocian a la respuesta de un líquido.
En 1867 J.C Maxwell, en su artículo “Sobre la teoría dinámica de los
gases”, incluido en la Enciclopedia Británica, propuso un modelo matemático
para describir los fluidos que poseen propiedades elásticas, es decir,
elementos asociados a la respuesta de un sólido:
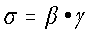
donde
b
es un parámetro semejante al módulo de rigidez ( Parámetro no-nulo). Tanto
la conducta que observó Weber en sólidos como Maxwell en líquidos se
denominó posteriormente “Viscoelasticidad”.
Después de Maxwell no se profundizó más en
el estudio hasta la segunda década del siglo XX, apareciendo una serie de
modelos lineales (flujo plástico y punto de fluidez) y no lineales de
comportamiento.
A partir de la Segunda Guerra Mundial, la Reología
cobró mucha fuerza con la búsqueda de materiales viscoelásticos para
lanzallamas. Aparecieron poco a poco modelos que asumieron que tanto el
módulo de rigidez podían variar con la tensión aplicada. Además se observó
que la viscosidad también dependía del tiempo ( Tixotropía y Reopexia) y se
profundizó en que los materiales reales pueden presentar comportamiento
viscoso, elástico, o una combinación de ambos.
En 1945 M. Reiner definió el número de Deborah, De
como:
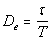
En donde “
t”
es el tiempo característico del material y “ T” el tiempo característico del
proceso de deformación. Si De era muy alto se consideraba al
material como un sólido elástico, y si De era muy bajo se le
consideraba como un líquido viscoso.
A partir de ese año, el interés por la
reología fue aumentando con la aparición de las fibras sintéticas,
plásticos, detergentes, aceites multigrado, pinturas y adhesivos entre
otros, estudiándose para ello suspensiones newtonianas tanto diluidas como
concentradas.
La reología ha sido muy importante y lo
seguirá siendo para el desarrollo de múltiples industrias, como por ejemplo
la industria farmacéutica y alimentaria, así que es de gran relevancia un
estudio minucioso de ésta.
1.2 La
Viscosidad
1.2.1
Definición
La viscosidad se puede definir como una medida de la resistencia a la
deformación del fluido. Dicho concepto se introdujo anteriormente en la Ley
de Newton, que relaciona el esfuerzo cortante con la velocidad de
deformación (gradiente de velocidad).
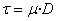(ecuación 1)
donde,
t
: esfuerzo cortante [mPa].
m : viscosidad [mPa·s]
D: velocidad de deformación [s-1]
1.2.2
Unidades
Las unidades de viscosidad más utilizadas son los milipascales por
segundo [mPa·s].
Se debe tener en cuenta que:
1000 mPa·s = 1 Pa·s
Además, el
sistema cegesimal aún se sigue usando, siendo la unidad de medida el
centiPoise [cp].
La conversión de unidades entre los dos
sistemas es:
1 cp = 1 mPa·s
1 Poise = 1 g/cm·s
La tabla siguiente es una aproximación del valor de la viscosidad para
sustancias muy conocidas a temperatura y presión ambientales [1]:
|
Fluidos |
Viscosidad aproximada (mPa·s) |
|
Vidrio |
1043 |
|
Vidrio Fundido |
1015 |
|
Betún |
1011 |
|
Polímeros fundidos |
106 |
|
Miel líquida |
104 |
|
Glicerol |
103 |
|
Aceite de oliva |
102 |
|
Agua |
100 |
|
Aire |
10-2 |
La reología ha sido muy importante y lo
seguirá siendo para el desarrollo de múltiples industrias, como por ejemplo
la industria farmacéutica y alimentaria, así que es de gran relevancia un
estudio minucioso de ésta.
1.2.3.
Aplicaciones del estudio de la Reología
-
Control de calidad de los alimentos: este control se realiza en la propia
línea de producción. Es determinante para la aceptación de productos como
patatas fritas, cereales, quesos, aperitivos, yogures, dulces, chocolates,
cremas, etc.
-
Estudio de la textura y consistencia de productos alimenticios: dichas
propiedades son muy importantes a la hora de que un producto sea del agrado
del consumidor.
-
Producción de pegamentos: el estudio de su plasticidad, de la forma de fluir
dentro del recipiente que lo contiene, etc.
-
Producción de pinturas: una pintura debe ser esparcida de forma fácil pero
sin que escurra.
-
Producción de productos cosméticos y de higiene corporal: la duración de una
laca sobre el pelo, la distribución de la pasta de dientes por toda la boca,
la forma de cómo se esparce una crema, etc. Todas estas características se
estudian con la reología para obtener la mayor eficacia del producto.
-
Producción de medicamentos: se estudia su estabilidad química, su tiempo de
caducidad y su facilidad de extrusión, entre otras.
-
Caracterización de elastómeros y de polímeros tipo PVC.
-
Estabilidad de emulsiones y suspensiones.
-
Caracterización de gasolinas y otros tipos de hidrocarburos.
-
Caracterización de metales (en situaciones de elevada temperatura), y de
cristales líquidos.
-
Control de sustancias que sean transportadas a lo largo de un recipiente
cilíndrico (para evitar la reopexia).
-
Estudio del magma en vulcanología: cuanto más fluido sea el magma más
tendencia va a tener el volcán a que provoque una erupción.
1.2.3
Tipos de viscosidad
Existen tres tipos de viscosidad [2]: la viscosidad
dinámica, la viscosidad cinemática y la viscosidad aparente.
La viscosidad dinámica o absoluta,
denominada “m”
se ha visto anteriormente en la ecuación 1.Si se representa la curva de
fluidez (esfuerzo cortante frente a velocidad de deformación) se define
también como la pendiente en cada punto de dicha curva.
En cambio, la viscosidad aparente “m”
se define como el cociente entre el esfuerzo cortante y la velocidad de
deformación. Este término es el que se utiliza al hablar de “viscosidad”
para fluidos no newtonianos (figura 1).
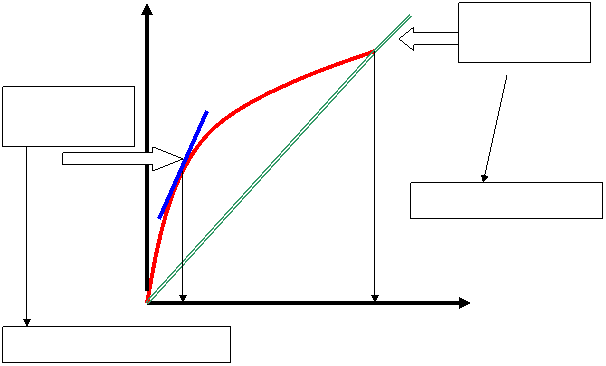
Figura 1: Curva de fluidez para representar la viscosidad dinámica y
aparente
Por último existe otro término de viscosidad “n“
denominado viscosidad cinemática, que relaciona la viscosidad
dinámica con la densidad del fluido utilizado. Las unidades más utilizadas
de esta viscosidad son los centistokes [cst].
1 stoke = 100 centistokes = cm2/s
Su ecuación es la siguiente:
Siendo:
n
: viscosidad cinemática.
m
: viscosidad dinámica .
r:
densidad del fluido.
1.2.4.
Variables que influyen en la viscosidad [1]
La viscosidad puede estar muy afectada por variables como el
gradiente de velocidad de deformación, la temperatura y la presión entre
otros, siendo éstas las más importantes.
Variación de la viscosidad con la velocidad de
deformación
Dicha variación se estudiará más adelante ya que va a ayudar a
clasificar los diferentes tipos de fluidos que se pueden encontrar desde el
punto de vista reológico. La siguiente tabla muestra el rango de gradientes
de velocidad de diversos procesos muy conocidos y sus aplicaciones [1].
|
Tipo de proceso |
Rango típico de gradiente de velocidad (s-1) |
Aplicaciones |
|
Sedimentación de partículas finas sobre un
líquido |
10-6- 10-4 |
Medicinas, pinturas |
|
Nivelación debido a tensión superficial |
10-2-10-1 |
Pinturas, tintas de impresión |
|
Escurrido bajo gravedad |
10-1-101 |
Dar mano de pintura, blanquear lavabos |
|
Extrusión |
100-102 |
Polímeros |
|
Amasado |
101-102 |
Alimentos |
|
Mezclado y agitado |
101-103 |
Líquidos |
|
Flujo en tuberías |
100-103 |
Bombeado |
|
Pulverizado y Pintado |
103-104 |
Secado en spray, pintura |
|
Fricción |
104-105 |
Cremas y lociones para piel |
|
Lubricación |
103-107 |
Motores de gasolina |
Variación de la viscosidad con la temperatura:
LÍQUIDOS
La
viscosidad disminuye con la temperatura. Existen varias fórmulas que
permiten evaluar la variación de la viscosidad de un líquido al cambiar la
temperatura. Las más importantes son:
A) La ecuación de Arrhenius
(ecuación 2)
siendo:
m : viscosidad dinámica [mPa·s]
A y B: constantes dependientes del líquido
T: es la temperatura absoluta en ºC
Como se ve en la ecuación, la viscosidad disminuye con la temperatura.
Esto es debido al hecho de que, conforme aumenta la temperatura, las fuerzas
viscosas son superadas por la energía cinética, dando lugar a una
disminución de la viscosidad. Por este hecho se deben extremar las
precauciones a la hora de medir la viscosidad, teniendo en cuenta que la
temperatura debe permanecer prácticamente constante.
B) La ecuación de Poiseville (1840)
(ecuación 3)
donde
m0: la viscosidad
dinámica a 0 º C.
T: la temperatura en ºC.
a,b:
coeficientes constantes.
GASES
En cuanto a los gases, hay que decir que cuanto mayor es la
temperatura, mayor es la agitación y los choques de las moléculas del gas,
oponiéndose al movimiento (mayor fricción) y produciendo un aumento de la
viscosidad del gas.
Variación de la viscosidad con la temperatura y la presión:
De las
numerosas ecuaciones utilizadas para determinar la viscosidad en función de
la temperatura y la presión (para líquidos tipo aceites lubricantes), se
propone la de Barus:
(ecuación 4)
En esta
expresión:
m0
es la viscosidad a T0
y a presión atmosférica.
A: 1/430
B: 1/36
Variación de la viscosidad con la presión.
La
viscosidad (en líquidos) aumenta exponencialmente con la presión. El agua a
menos de 30 º C es el único caso en que disminuye. Los cambios de viscosidad
con la presión son bastante pequeños para presiones distintas de la
atmosférica. Para la mayoría de los casos prácticos, el efecto de la presión
se ignora a la hora de hacer mediciones con el viscosímetro.
1.3.
Clasificación de fluidos
1.3.1 INTRODUCCIÓN
Un fluido se define como una sustancia que
se deforma continuamente bajo la aplicación de esfuerzos cortantes.
Las características reológicas de un fluido son uno
de los criterios esenciales en el desarrollo de productos en el ámbito
industrial. Frecuentemente, éstas determinan las propiedades funcionales de
algunas sustancias e intervienen durante el control de calidad, los
tratamientos (comportamiento mecánico), el diseño de operaciones básicas
como bombeo, mezclado y envasado, almacenamiento y estabilidad física, e
incluso en el momento del consumo (textura).
Las propiedades reológicas se definen a partir de la
relación existente entre fuerza o sistema de fuerzas externas y su
respuesta, ya sea como deformación o flujo. Todo fluido se va deformar en
mayor o menor medida al someterse a un sistema de fuerzas externas. Dicho
sistema de fuerzas se representa matemáticamente mediante el esfuerzo
cortante “txy”
, mientras que la respuesta dinámica del fluido se cuantifica mediante la
velocidad de deformación “D”.
Como ejemplo se puede poner un elemento de fluido
entre dos placas paralelas infinitas, donde la placa superior se mueve a una
velocidad constante du bajo la influencia de una fuerza aplicada Fx
. La placa inferior permanece estática (Figura 1). El movimiento de la
placa superior da lugar a un gradiente de velocidad en el fluido. Esta
geometría puede ser usada para definir un parámetro reológico fundamental,
el esfuerzo cortante o de cizalladura. Dicho esfuerzo se define como la
fuerza por unidad de área necesaria para alcanzar una deformación dada,
viniendo reflejado en la siguiente expresión:
donde
dAy
es el área del elemento de fluido en contacto con la placa. Las unidades del
esfuerzo cortante son “mPa”.
Hay que buscar una alternativa para obtener el
esfuerzo cortante de forma que sea medible fácilmente.
Figura 1: Detalle del movimiento del fluido.
Durante un intervalo de tiempo
dt
el elemento de fluido se deforma desde la posición inicial M a la posición M’
(de P a P’), variando un cierto ángulo
da.Con
la deformación aparece una cierta velocidad, denominada velocidad de
deformación. Se define como el cambio de velocidad entre las dos placas, y
su expresión es:
D = limdt->0(da/dt)
= (da/dt)
Sustituyendo este
último término por otro mejor medible se puede calcular el esfuerzo cortante
de una forma sencilla. Para ello, se puede ver en la figura que la distancia
dl
entre los puntos M y M’ es:
dl=
du·dt
siendo
du
la velocidad de la placa superior y
dt
el tiempo que tarda el fluido en deformarse de M a M’.De manera alternativa
para ángulos pequeños se ve que:
dl
=
dy·
da
Igualando ambas expresiones se obtiene:
da/dt
=
du/dy
A continuación se toman límites a ambos lados y se
llega a la siguiente ecuación:
da/dt
=du/dy= D
Por lo tanto, el elemento de fluido de la figura ,
cuando se somete a un esfuerzo cortante “dFx/dAy”
experimenta una velocidad de deformación dada por “du/dy”.
1.3.2 TIPOS DE FLUIDOS:
Existen 3 tipos de fluidos [4]:
q
Newtonianos
(proporcionalidad entre el esfuerzo cortante y la
velocidad de deformación).
q
No Newtonianos
(no hay proporcionalidad entre el esfuerzo
cortante y la velocidad de deformación)
q
Viscoelásticos
(se comportan como líquidos y sólidos, presentando
propiedades de ambos).
La relación entre el esfuerzo cortante aplicado y la
velocidad viene dada por la ecuación:
(Ley de viscosidad de Newton)
siendo:
txy
= esfuerzo cortante (mPa)
m
= viscosidad dinámica del fluido (mPa·s)
du/dy = velocidad de deformación del
fluido (s-1) = D
(estas unidades son las más utilizadas en reología)
Un esquema conciso de los tipos de fluidos existentes
en Reología es el siguiente:
TIPOS DE FLUIDOS
-
1.NEWTONIANOS
- NO NEWTONIANOS
-
•Independientes del Tiempo
• Pseudo plástico
•Dilatantes
•Tixotropicos
•Reopécticos
3. VISCOELASTICO
A continuación se
va a describir detalladamente cada uno de ellos:
-FLUIDOS
NEWTONIANOS
Un fluido newtoniano se caracteriza por cumplir la Ley
de Newton, es decir, que existe una relación lineal entre el esfuerzo
cortante y la velocidad de deformación (ecuación anterior). Si por ejemplo
se triplica el esfuerzo cortante, la velocidad de deformación se va a
triplicar también. Esto es debido a que el término
m
(viscosidad) es constante para este tipo de fluidos y no depende del
esfuerzo cortante aplicado.
Hay que tener en cuenta también que la viscosidad de un
fluido newtoniano no depende del tiempo de aplicación del esfuerzo, aunque
sí puede depender tanto de la temperatura como de la presión a la que se
encuentre.
Para una mejor comprensión de este tipo de fluido se
representan dos tipos de gráficas, la“Curva de Fluidez” y la“Curva
de Viscosidad”. En la Curva de Fluidez se grafica el esfuerzo cortante
frente a la velocidad de deformación (
t
vs D), mientras que en la Curva de Viscosidad se representa la viscosidad en
función de la velocidad de deformación (m
vs D). Para un fluido newtoniano se obtienen las siguientes curvas (Figura
2):
Como se puede observar en la curva de fluidez , el
valor de la viscosidad
m
es la tangente del ángulo que forman el esfuerzo de corte y la velocidad de
deformación, la cual es constante para cualquier valor aplicado. Además se
observa en la curva de viscosidad que la viscosidad es constante para
cualquier velocidad de deformación aplicada.
La ecuación que modela un fluido newtoniano es la vista
anteriormente.
Ejemplos de este tipo
de fluidos son el agua, el aceite (Figura 3), etc.
Figura 3: El aceite de oliva, ejemplo de fluido
newtoniano.
- FLUIDOS NO NEWTONIANOS:
Los fluidos no newtonianos son aquellos en los que la relación
entre esfuerzo cortante y la velocidad de deformación no es lineal. Estos
fluidos a su vez se diferencian en dependientes e independientes del
tiempo.
a)Fluidos independientes del tiempo
de aplicación:
Estos fluidos se pueden clasificar dependiendo de si tienen o no
esfuerzo umbral, es decir, si necesitan un mínimo valor de esfuerzo cortante
para que el fluido se ponga en movimiento.
Fluidos sin esfuerzo umbral
Fluidos
pseudoplásticos: (SHEAR-THINNING)
Este tipo de fluidos se caracterizan por una disminución de su
viscosidad, y de su esfuerzo cortante, con la velocidad de deformación.
a)
FLUJO DE VARILLAS RÍGIDAS SUSPENDIDAS EN UN LÍQUIDO NEWTONIANO :
Como se puede observar en la figura, existen una serie
de varillas desorientadas dentro del líquido newtoniano. Cada varilla,
caracterizada por su movimiento browniano, tiene un vector de velocidad que
tiende a adoptar una situación horizontal Dicho movimiento browniano
(propuesto por Brown en 1827) es una observación indirecta de la agitación
térmica de las moléculas de un líquido, al visualizarse el desplazamiento de
partículas en suspensión en el seno del mismo.
La resultante de los choques al azar es una fuerza de
magnitud y dirección variable que a la orientación de las varillas,
responsable de la viscosidad, para evitar que se llegue a un cierto estado
de equilibrio. Cuanto mayor sea la orientación de las varillas, menor será
la viscosidad del fluido (Figura 5).
b)
FLUJO DE MOLÉCULAS FILAMENTARIAS EN UN LÍQUIDO NEWTONIANO
Se supone que, dentro de un fluido newtoniano situado
entre dos placas paralelas, una de las cuales se mueve, aparecen una serie
de macromoléculas en forma de filamentos porosos que contienen grupos de
átomos con una gran movilidad.
Al principio estos grupos de átomos forman
filamentos bastante enredados. Con el tiempo, al moverse la placa superior,
la velocidad de deformación aumenta y la resultante de las fuerzas tiende a
desenredar estos filamentos en la dirección del flujo, dependiendo de su
elasticidad y de su velocidad de deformación, y además dicha fuerza libera
parte del líquido que existe alrededor de la molécula.
Como resultado de todo lo que ocurre en el seno del
fluido se produce una disminución de la fricción interna dando lugar a su
vez a una disminución de la viscosidad (Figura 6).
Ejemplos de fluidos
pseudoplásticos son: algunos tipos de ketchup (Figura 7), mostaza, algunas
clases de pinturas, suspensiones acuosas de arcilla, etc.
Figura 7: El ketchup como ejemplo de fluido
pseudoplástico .
La formulación matemática de un fluido
pseudoplástico es bastante compleja aunque para movimiento simple se pueden
utilizar varias formulas [1]
1)
Ley de potencia (Ostwald) :
siendo:
t
: el esfuerzo cortante [mPa].
D: la velocidad de deformación [s-1]
K: constante cuyas dimensiones dependen del
valor de n (viscosidad aparente)
n: valor entero menor que uno.
Se puede calcular el valor de “n” representando la
ecuación en escala logarítmica :
La ordenada en el origen que se obtiene
representa el valor de K.
La segunda forma de la ecuación se utiliza para evitar
que salga negativo cuando el movimiento es distinto al estado simple:
2)
Series de potencia (Steiger, Ory):
Fluidos
dilatantes: (SHEAR-THICKENING)
Los fluidos dilatantes son suspensiones en las que se
produce un aumento de la viscosidad con la velocidad de deformación, es
decir, un aumento del esfuerzo cortante con dicha velocidad. La figura 8
representa las curvas de fluidez y viscosidad para este tipo de fluidos:
El fenómeno de dilatancia se produce debido al fase dispersa del
fluido. En dicho fluido tiene lugar un empaquetamiento de las partículas,
dejando a la fase continua casi sin espacio.
Si a
continuación se aplica un esfuerzo, el empaquetamiento se altera y los
huecos entre las partículas dispersas aumentan. Además, conforme aumenta la
velocidad de deformación aplicada, mayor turbulencia aparece y más difícil
es el movimiento de la fase continua por los huecos, dando lugar a un mayor
esfuerzo cortante (la viscosidad aumenta).
Ejemplos
de este tipo
de fluidos son: la harina de maíz (Figura 9), las disoluciones de
almidón muy concentradas, la arena mojada, dióxido de titanio, etc.
Figura 9: Bote de harina de maíz. Mezclada con agua da
lugar a una masa que se vuelve muy espesa al
moverla.
La ecuación matemática que
describe un
comportamiento dilatante es la ley de la potencia vista anteriormente en el
caso de fluidos pseudoplásticos (ecuación 1), cambiando únicamente el valor
de n ,que debe ser menor que la unidad.
(n < 1)
Fluidos con esfuerzo umbral, llamados también plásticos (VISCOPLASTIC)
Este tipo de fluido se comporta como un sólido hasta que
sobrepasa un esfuerzo cortante mínimo (esfuerzo umbral) y a partir de dicho
valor se comporta como un líquido. Las curvas de fluidez y viscosidad se
representan en la figura 10:
La razón por la que se comportan así los fluidos
plásticos es la gran interacción existente entre las partículas
suspendidas en su interior, formando una capa llamada de solvatación.
Están formados por dos fases, con una fase dispersa formada por sólidos y
burbujas distribuidos en una fase continua .
En estos fluidos, las fuerzas de Van der Waals y los
puentes de hidrógeno, producen una atracción mutua entre partículas. También
aparecer fuerzas de repulsión debidas a potenciales de la misma polaridad.
En este tipo de fluidos se forman coloides cuyas fuerzas
repulsivas tienden a formar estructuras de tipo gel Si las partículas son
muy pequeñas poseen entonces una gran superficie específica, rodeados de una
capa de adsorción formada por moléculas de fase continua.
Gracias a esta capa, las partículas inmovilizan gran cantidad de fase
continua hasta que no se aplica cobre ellas un esfuerzo cortante
determinado.
Los fluidos plásticos, a su vez, se diferencian en la existencia
de proporcionalidad entre el esfuerzo cortante y la velocidad de
deformación, a partir de su esfuerzo umbral. Si existe proporcionalidad, se
denominan fluidos plásticos de Bingham y si no la hay, se denominan solo
plásticos.
Algunos
ejemplos de comportamiento plástico son el
chocolate, la arcilla, la mantequilla, la mayonesa, la pasta de dientes
(Figura 11), las emulsiones, las espumas, etc.
Figura 11: Ejemplo típico de fluido plástico
Las ecuaciones que modelan el comportamiento de los
fluidos plásticos son dos:
1)
Ecuación generalizada de Bingham:
Se aplica a los fluidos plásticos de Bingham:
con
t:
esfuerzo cortante (Pa)
ty:
esfuerzo umbral requerido para que el flujo se ponga en movimiento (Pa).
Representa el valor del esfuerzo cortante para
velocidad de deformación nula
m:
viscosidad aparente (Pa·s)
D: velocidad de deformación (s-1)
n: valor entero
2)
Ecuación de Casson:
Se aplica para aquellos fluidos en los que no existe
proporcionalidad entre el esfuerzo y la velocidad:
Siendo
t:
esfuerzo cortante (Pa)
ty:
esfuerzo umbral (Pa)
D: velocidad de deformación (s-1)
m:
viscosidad plástica definida por Casson
b)
Fluidos dependientes del tiempo de aplicación:
Este tipo de fluidos se clasifican en dos tipos: los
fluidos tixotrópicos, en los que su viscosidad disminuye al aumentar
el tiempo de aplicación del esfuerzo cortante, recuperando su estado inicial
después de un reposo prolongado, y los fluidos reopécticos, en los
cuales su viscosidad aumenta con el tiempo de aplicación de la fuerza y
vuelven a su estado anterior tras un tiempo de reposo.
FLUIDOS TIXOTRÓPICOS
Los fluidos tixotrópicos se caracterizan por un cambio
de su estructura interna al aplicar un esfuerzo. Esto produce la rotura de
las largas cadenas que forman sus moléculas .
Dichos fluidos, una vez aplicado un estado de cizallamiento
(esfuerzo cortante), sólo pueden recuperar su viscosidad inicial tras un
tiempo de reposo.
La
viscosidad va disminuyendo al aplicar una fuerza y acto seguido vuelve a
aumentar al cesar dicha fuerza debido a la reconstrucción de sus estructuras
y al retraso que se produce para adaptarse al cambio. Aparece un fenómeno
de Histéresis (Figura 12) .
Figura 12: Curvas de fluidez y de viscosidad de un
fluido tixotropía (hay histéresis)
Las razones de este
comportamiento son diversas [4]. Si se considera al fluido como un sistema
disperso, se debe tener en cuenta que las partículas que hay en él poseen
diferentes potenciales eléctricos y tienden a formar tres estructuras
variadas dependiendo de cómo sea la fase dispersa.
Si la fase dispersa
está formada por una serie de capas se denomina “Castillo de cartas ,
Card House ” (Figura 13), si en cambio se compone de una serie de
varillas se denomina “Armadura” (Figura 14), y si la fase dispersa está
compuesta por formas esféricas se denomina “Estructura de perlas
encadenadas”(Figura 15).Las fuerzas que actúan en estas estructuras son de
tipo electrostático y se originan por el intercambio de iones dentro del
fluido, el cual provoca atracciones y repulsiones entre ellos que dan lugar
a cambios estructurales.
Figura 13: Fase
dispersa tipo Card House o “Castillo de cartas”
Figura 14: Fase
dispersa denominada de “Armadura”
Figura 15: “Estructura tipo perlas encadenadas”.
Estos cambios
estructurales hacen disminuya la viscosidad con el aumento de la velocidad
de deformación y que ésta esté muy influenciada por el tiempo. La estructura
puede volver a recuperar su forma inicial dejándola un tiempo en reposo.
Para
diferenciar de forma sencilla un fluido tixotrópico, se aumenta la velocidad
de deformación hasta un determinado valor y luego se disminuye hasta el
reposo, observando entonces un fenómeno de histéresis, que ayuda a
comprender la variación de la viscosidad.
Ejemplos
típicos se fluidos tixotrópicos son: las pinturas, el yogur (Figura 16),
las tintas de impresión, la salsa de tomate, algunos aceites del petróleo,
el nylon, etc.
Figura 16: El yogur es un buen ejemplo de fluido
tixotrópico
Para modelizar la
variación de la viscosidad con el tiempo, [1] se ideó la siguiente ecuación
:
donde,
siendo,
II : el tiempo de
relajación del fluido, es decir, el tiempo que tarda el fluido en
disminuir su tensión a 1/e veces. Puede haber diversos tiempos de
relajación.
R(II) : función de
distribución de tiempos de relajación .
m0
: viscosidad inicial sin perturbaciones.
F(D2) :
función simétrica de la velocidad de deformación.
FLUIDOS REOPÉCTICOS
Los fluidos
reopécticos, en cambio, se caracterizan por tener un comportamiento
contrario a los tixotrópicos, es decir, que su viscosidad aumenta con el
tiempo y con la velocidad de deformación aplicada y presentan una histéresis
inversa a estos últimos.
Esto es
debido a que si se aplica una fuerza se produce una formación de enlaces
intermoleculares conllevando un aumento de la viscosidad, mientras que si
cesa ésta se produce una destrucción de los enlaces, dando lugar a una
disminución de la viscosidad.
Las curvas
de fluidez y de viscosidad de los fluidos reopécticos se representan en la
figura 17:
Existen pocos fluidos de
este tipo. Algunos ejemplos son: el yeso (Figura 18) y la arcilla
bentonítica, entre otros.
Figura 18: El yeso
mezclado con el agua da lugar a un fluido reopéctico, endureciéndose
muy rápidamente
FLUIDOS
VISCOELÁSTICOS:
Los fluidos
viscoelásticos se caracterizan por presentar a la vez tanto propiedades
viscosas como elásticas. Esta mezcla de propiedades puede ser debida a la
existencia en el líquido de moléculas muy largas y flexibles o también a la
presencia de partículas líquidas o sólidos dispersos.
La ecuación que describe
el comportamiento viscoelástico está basada en el modelo de Maxwell:
donde,
t:
esfuerzo cortante aplicado.
l:
tiempo de relajación.
:gradiente
de esfuerzos cortantes (m/G).
m:
viscosidad aparente.
D: velocidad de
deformación.
Éste modelo se puede
representar como el modelo mecánico de la siguiente figura:
Ejemplos de fluidos
viscoelásticos son la nata, la gelatina, los helados (Figura 19), etc.
Figura 19: El helado
muestra propiedades sólidas y líquidas a
la vez (Viscoelástico)
Articulo
relacionado con la Reología de los alimentos
RETORNAR A PAGINA PRINCIPAL
