Relaciones interespecíficas
Cuando las especies comparten un ambiente pueden desarrollar interacciones entre sí, estas pueden beneficiarlas o perjudicarlas.
La relación depredador - presa
Depredación : Cuando los miembros de una población se alimentan de los de otra población, no siempre significa la muerte de la presa.
Cuatro tipos de depredadores :
- Herbívoros
- Carnívoros
- Caníbales
- Parásitos
| Idea básica : La población de depredadores depende absolutamente de las presas. | |
| El comportamiento del sistema depende de la densidad de ambas poblaciones. |

Estudio matemático : Volterra, Lotka, y Gaus
| Dinámica semejante : ley de acción de masas de la química, lo cambios se hacen proporcionales al producto de las concentraciones de los elemento que reaccionan o actúan recíprocamente. | |
| La posibilidad de un depredador que encuentre y devore puede hacerse proporcional al producto de las densidades del depredador y la presa (simplificación burda). | |
| La organización de las comunidades hace que las probabilidades de interacción se aparten más o menos del simple producto de las densidades. | |
| Dispositivos de defensa de las posibles presas. | |
| Adaptaciones para asegurar la localización de las presas |
FORMULACIÓN MATEMÁTICA :
Supuestos :
La población presa encuentra siempre alimento, el suministro de alimento de la población del depredador depende enteramente de la población presa.
El ambiente no cambia en favor de una especie y que la adaptación genética es suficientemente lenta.
t = tiempo

Roughgarden (1979)
V : tamaño de la población de presas.
P : Tamaño de la población de depredadores.

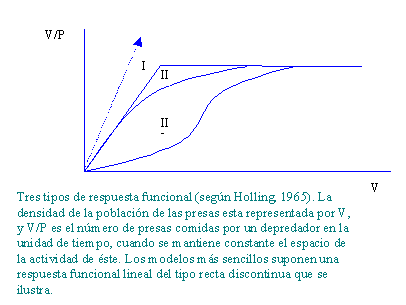
Holling (1965) respuestas :
- Son raras. Crustáceos que se alimentan de algas unicelulares.
- Depredadores invertebrados. El depredador toma cierto tiempo para capturar y matar.
- Depredadores vertebrados. Los depredadores aprenden a elegir entre las presas diferentes especies que están disponibles.
MODELO SENCILLO :
Supuestos :
- Que la presa crece en forma exponencial en ausencia del depredador ;
- una respuesta funcional lineal para el depredador ;
- que la respuesta numérica es un número constante de veces la respuesta funcional y
- una tasa de muerte constante en los depredadores.
dv/dt = rV - (aV)P.
dP/dt = b(aV)P - dP.
Estas ecuaciones se conocen como ecuaciones de Lotka y Volterra. Su expresión gráfica produce unas curvas de comportamiento oscilatorio, típicas de los sistemas depredador presa.
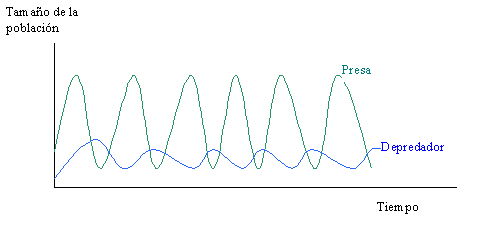
Comportamiento típico del sistema depredador - presa, según el modelo de Lotka y Volterra.