Estructura y dinámica de las poblaciones
| Una población está formada por un conjunto de individuos de la misma especie y que tienen una historia en común. | |
| La estructura de una población generalmente está referida a : |
Estructura de sexos (razón de sexos).
Estructura de Edades (Biológicas o cronológicas).
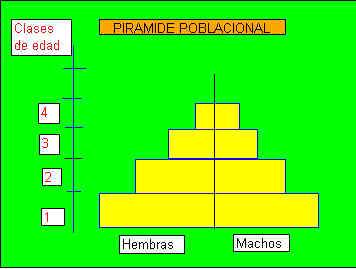
| Una pirámide poblacional es una manera conveniente de representar sexos y edades simultáneamente. | |
| En algunos casos contribuyen a la estructura de la población la organización social. |
Procesos que hacen posible la dinámica
Natalidad incrementan la población
Inmigración
Mortalidad disminuyen la población
Emigración
Balance : factores que hacen crecer = factores que hacen disminuir Þ estado estacionario, la población se mantiene constante pero dinámica.
Tasas de mortalidad y natalidad
Son modelos que expresan el crecimiento de las poblaciones exponencial y logístico.
Estrategias de crecimiento poblacional :
Estrategia de la "r"
Estrategia de la "k"
Población : conjunto de individuos de la misma especie.
Comparten :
| Similitudes morfológicas | |
| área de distribución | |
| historia común |
Con una organización y dinámica que le permiten sobrevivir
Ejemplo :
| Población de truchas de un lago | |
| población de moscas de un establo. |
La suma de individuos con cierta estructura y dinámica, estructura de sexos y edades en un espacio o lugar determinado.
Estructura de sexos
Razón de sexos = # machos de una población / # hembras de una población.
Estructura de edades
Se clasifican a los individuos en grupos definidos :
Edades cronológicas - tiempo -.
Mamíferos : años
aves : meses
insectos : días
bacterias : horas
Edades biológicas - periodos de vida - categorías.
| Cría | huevo |
| juvenil | larva |
| adulto | pupa |
| senil | adulto |
Estructura social
Vertebrados superiores : vicuñas se agrupan en familias y tropías de machos.
Insectos : se agrupan en función al trabajo formando castas, la reproductora (reina y rey) y trabajadoras (obreras).
Pirámide poblacional
|
Dinámica
Las poblaciones experimentan procesos que hacen variar el número de individuos y que cuando se compensan entre si el número el tamaño se mantiene constante.
La Mortalidad y la natalidad se pueden expresar en tasas porcentuales y diferenciales.
Los procesos que hacen cambiar a las poblaciones son : emigración, inmigración, natalidad y mortalidad.
Mortalidad : Nº de individuos muertos.
Natalidad : Nº de individuos nacidos.
En un periodo de tiempo, en relación al Nº al número de individuos al inicio del periodo de tiempo.
La natalidad y la mortalidad se dan en forma simultánea y su diferencia mostrará que la población crezca o disminuya.
Cuando las tasas de natalidad o mortalidad se expresan en tasas diferenciales, en un tiempo infinitamente pequeño, se suelen usar las letras:
b : natalidad
-m : mortalidad
r = b - m
r = Índice reproductor neto o tasa intrínseca de aumento natural.
Efecto de la natalidad :
dN / dt = bN
Efecto de la mortalidad :
dN / dt = -mN
Efecto conjunto :
dN / dt = (b - m)N
dN / dt = rN
donde : r = b + (-m)
r = b - m
r = tasa intrínseca de aumento natural
El potencial biótico de una especie se define cuando la natalidad se hace máxima y la mortalidad se hace mínima.
Integrando :
Nt = Noert
Donde :
Nt = Nº de individuos en el tiempo t
No = Nº inicial de individuos
e = base de logaritmos neperianos
r = índice intrínseco de crecimiento poblacional o tasa intrínseca de aumento natural.
t = intervalo de tiempo
Si la natalidad supera siempre a la mortalidad, el valor de "r" será siempre positivo y la población experimentará un crecimiento.
Modelos de crecimiento
Modelo exponencial.
- Supone : crecimiento continuo e indefinido (retroalimentación positiva)
dN/dt = rN
N = # de individuos de la población, t = tiempo durante el cual se dará el crecimiento, índice reproductor neto expresado como tasa diferencial, d = diferencial de...
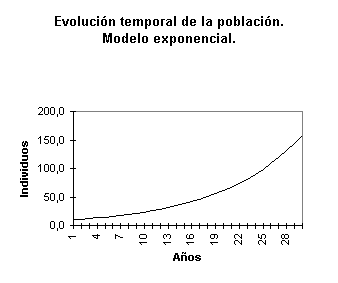
Por cada unidad de tiempo que pase la población se multiplicara por una cantidad constante, mientras más grande será N mayor será el crecimiento.
Ejemplos:
Una población de vizcachas en enero de 1991 tenía 200 individuos y en enero de 1992 se produjeron 40 muertes y 80 nacimientos. Hallar las tasas porcentuales anuales de natalidad y mortalidad y calcule el tamaño final de la población suponiendo que no hubo migración.
Un población de vicuñas presenta un crecimiento exponencial (condiciones óptimas) en cuantos años alcanzará una población de 500 individuos. Si r = 1.2 y No = 50 individuos.
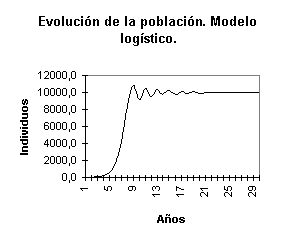
Modelo logístico.
Supone que la población no crece indefinidamente y mientras mayor sea su densidad más lento será el crecimiento, se detendrá cuando la población alcance un límite denominado capacidad de carga.
Experimenta retroalimentación negativa, la población crece solo hasta un límite, la capacidad de carga, y cuando se supera disminuirá su tamaño.
Una población esta influenciada en su mayor o menor grado por el medio ambiente, esto manifiesta en el tamaño y el crecimiento de la población
 dN/dt =
rN[ (k-N)/k]
dN/dt =
rN[ (k-N)/k]
Programas de simulación en dinámica de poblaciones.
| Crecimiento poblacional Gecko | |
| Gecko home page. | |
| CourseWare Java toolkit home page. | |
| BacSim home page. |
Modelos poblacionales
1.- Modelo fenomenológico:
|
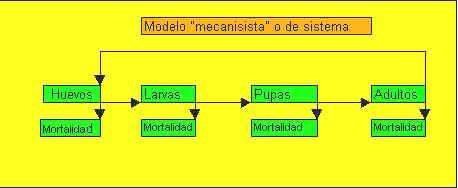
2.- Modelo "mecanisista o de sistemas"
1.- Modelo "mecanisista". Dinámica de sistemas |
2.- Modelo gráfico |
3.- Modelo matemático |
| 4.- Simulación |
| Contextos de operación | Variables del entorno |
| Población | ¿Cómo cambia? |
| Procesos de regulación denso dependiente |
|
|
|
En el diagrama anterior:
Compartimentos: Variables de estado. Ej. número de larvas.
Variables de flujo: Ej. tasa de conversión de huevos a larvas (TCHV).
TCHL= f(Temperatura, pp., enemigos naturales, etc.)
Las variables de flujo pueden ser expresadas mediante una o más fórmulas matemáticas.
Existirán tantos modelos como la cantidad de modelistas, serán representaciones mas reales de la dinámica de las poblaciones en la naturaleza.